微机原理与接口技术(一)
计算机的过程控制:
- 计算机硬件技术
- 输入输出接口控制技术(计算机的基础知识、微型计算机基本原理、微机接口控制)
第一章 微型计算机系统
计算机系统:软件系统、硬件系统
硬件系统:主机系统、外部设备
外部设备:所有可以通过输入输出接口与计算机进行信息交换的电子设备。
主机系统:CPU、存储器、输入输出接口、总线
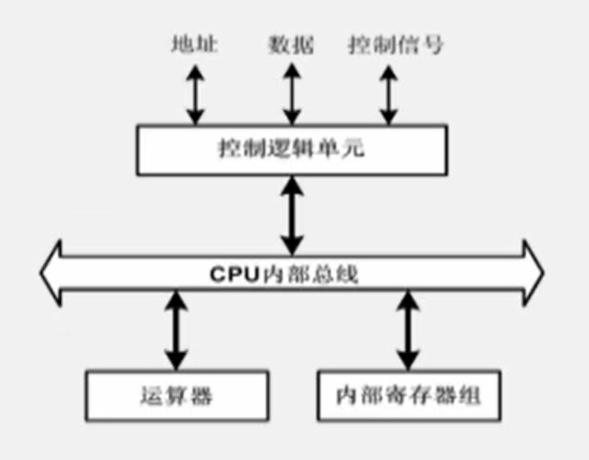
一、微处理器(CPU)
- 微处理器简称CPU,是计算机的核心
- 主要包括:运算器、控制器、寄存器组
二、存储器
定义:计算机的记忆装置,用于存放计算机工作过程中需要操作的数据和程序
存储器:内存储器、外存储器
外存储器:
联机外存——硬磁盘
脱机外存——各种移动存储设备
内存储器
特点:存取速度较快,容量相对较少
内存按单元组织,每单元都对应一个唯一的地址
每个内存单元中存放1Bytc数据
内存单元个数称为内存容量
内存储器:
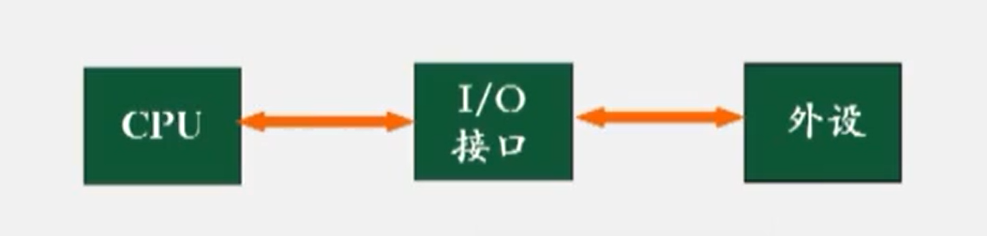
存储容量:存放的数据量,用字节表示,每8位0或1称为1字节(Byte)
对存储器的操作:读(出),写(入) 信息交换
读:将内存单元的内容取入CPU,原单元内容不变
写:CPU将信息放入内存单元,单元中原来的内容被覆盖
内存储器的分类
按工作方式可分为:随机存取存储器(RAM)、只读存储器(ROM)
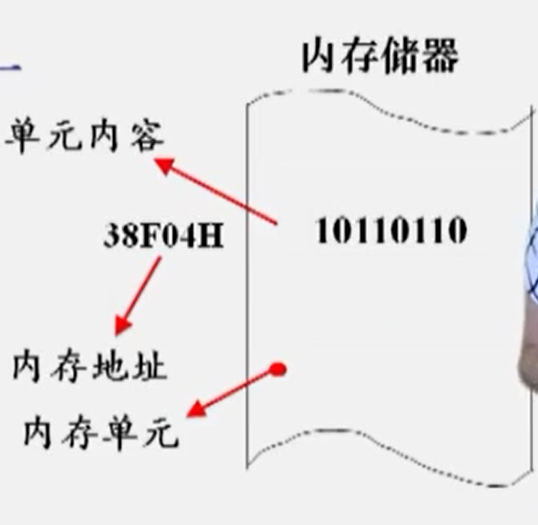
三、输入/输出接口
接口是CPU与外部设备间的桥梁
主要功能:
- 数据缓冲寄存
信号电平或类型的转换
- 现实主机与外设见的运行匹配
见图3
四、总线(BUS)
- 是一组导线和相关的控制驱动电路的集合
- 是计算机系统各部件之间传输地址、数据和控制信息的通道
- 地址总线(AB)、数据总线(DB)、控制总线(CB)
软件系统
软件:为运行管理和维护计算机系统或为实现某一功能而编写的各种程序的总和及其相关资料
软件:应用软件、系统软件
系统软件:操作系统、编译系统、网络系统、工具软件
见图4
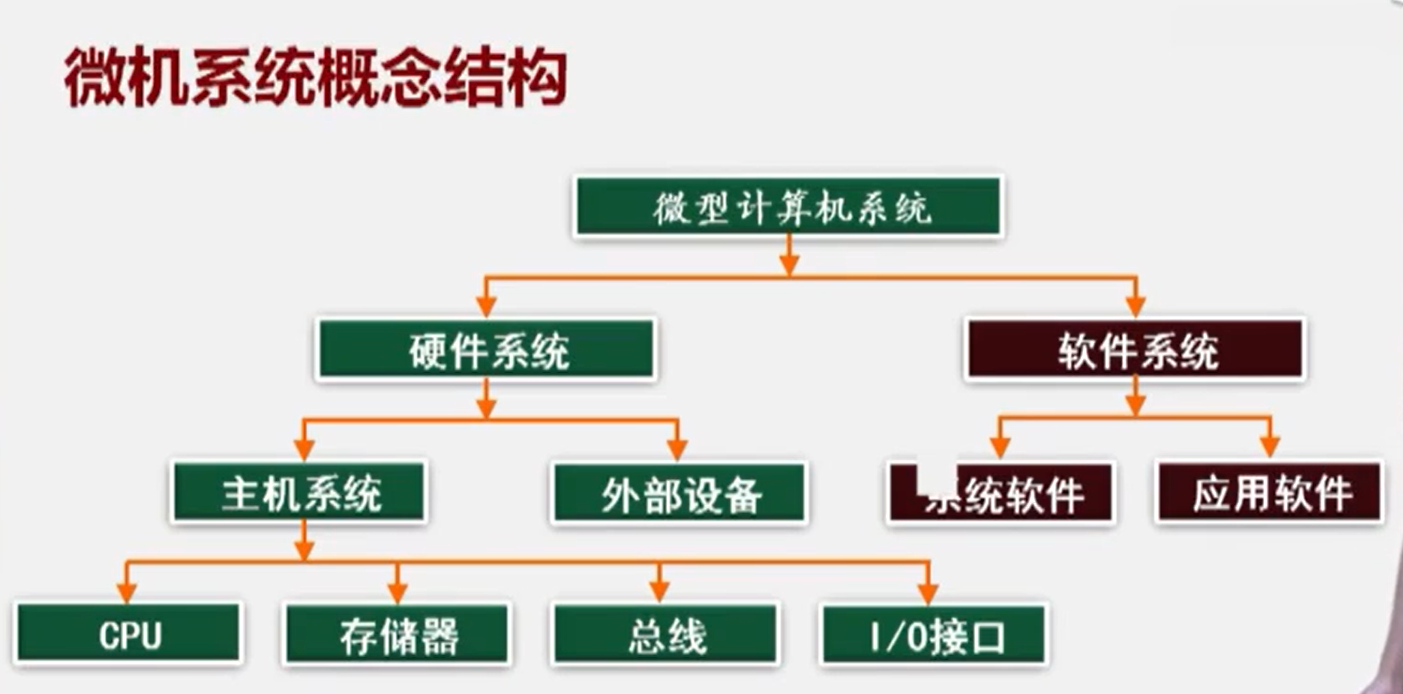
主机系统特征
能够与CPU直接进行信息交换的部件属于主机系统
不能够与CPU直接进行信息交换的部件属于外部设备
微型计算机的一般工作过程
微机中指令的执行过程
指令:由人向计算机发出的能够为计算机所识别的命令
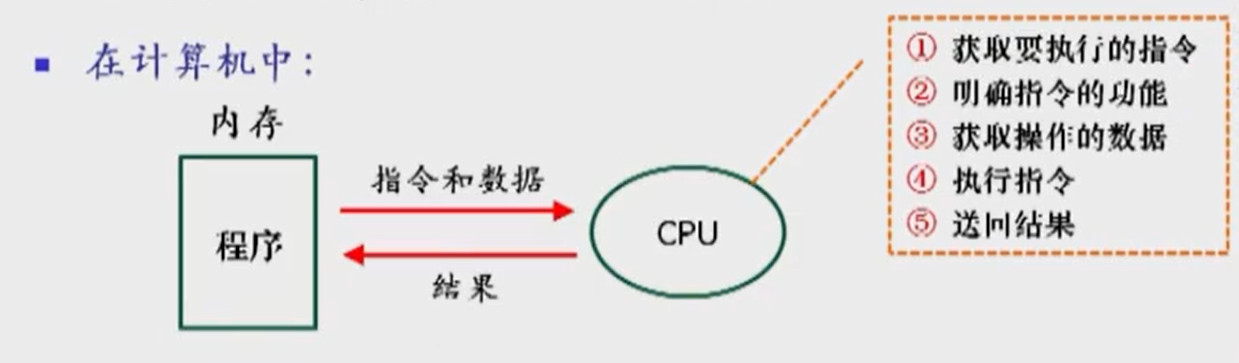
计算机的工作是逐条执行由指令构成的程序
程序是指令的序列
- 计算机的工作过程就是指令执行的过程
见图5、6
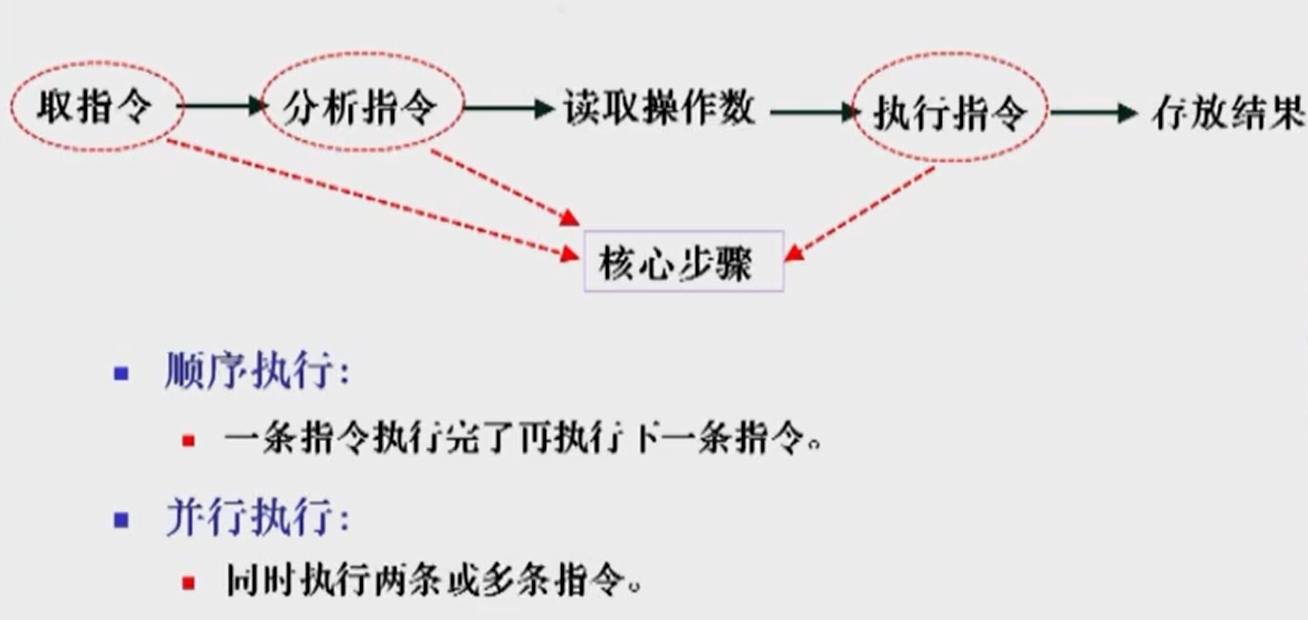
顺序执行方式
见图7

- 执行时间=取指令+分析指令+执行指令
- 设:三个部分的执行时间均为△t,则:执行n条指令时间T₀为:
- T₀=3n△t
并行流水线工作方式
见图8
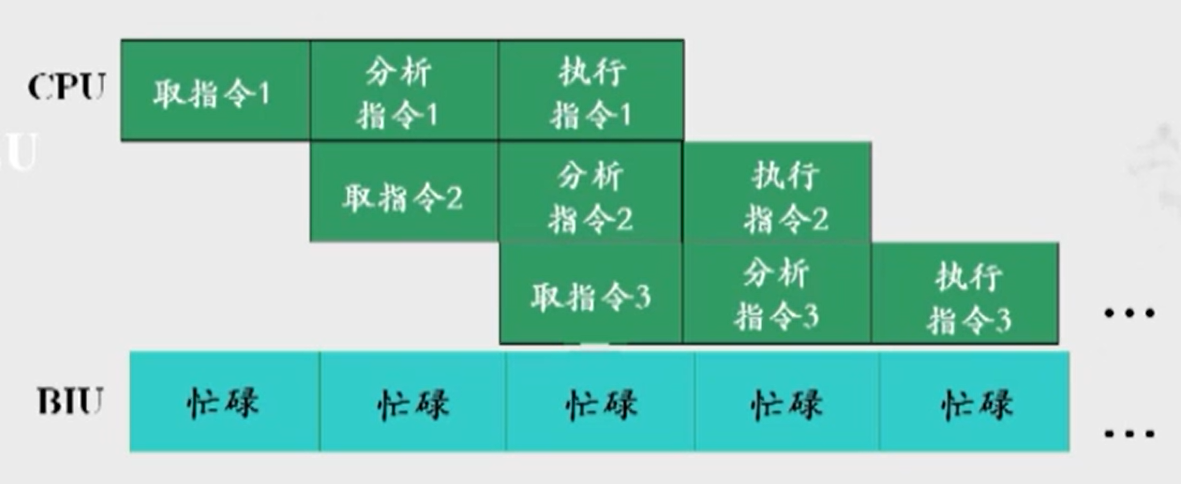
- 仅第一条指令需要3△t,就有一条指令执行结束
- 执行时间:T=3△t+(n-1)△t
两种执行方式时间的比较
并行
- 更高的效率,更高的复杂度
相对与顺序执行方式,指令并行执行的优势用加速比S表示:
- 例:
- 3n △t / ( 3 △t + (n-1) △t )
- -3n / (2+n)
- 例:
冯诺伊曼计算机
冯诺伊曼计算机的工作原理
存储程序工作原理
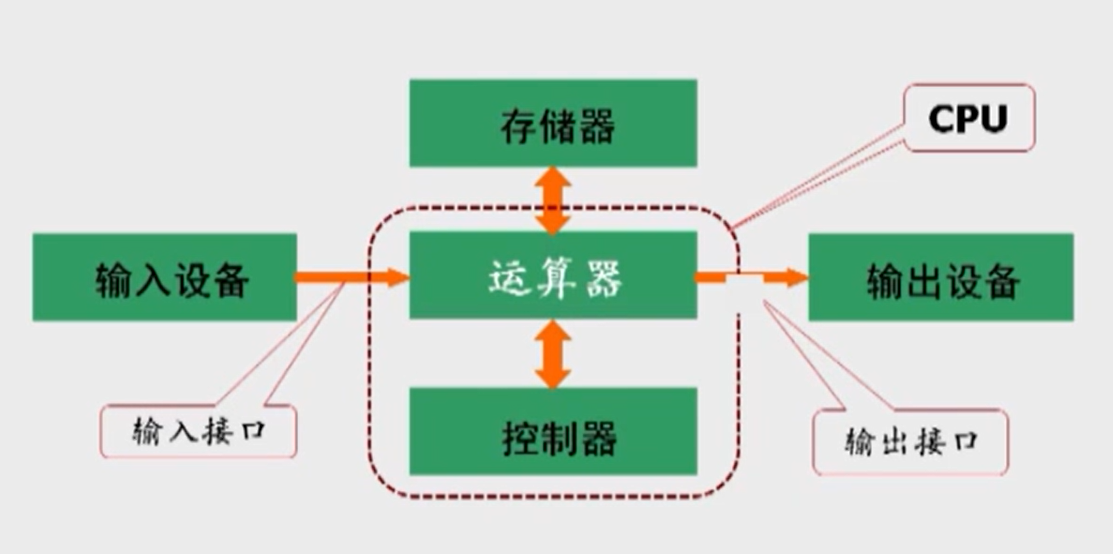
结构特点
运算器为核心
见图9、10
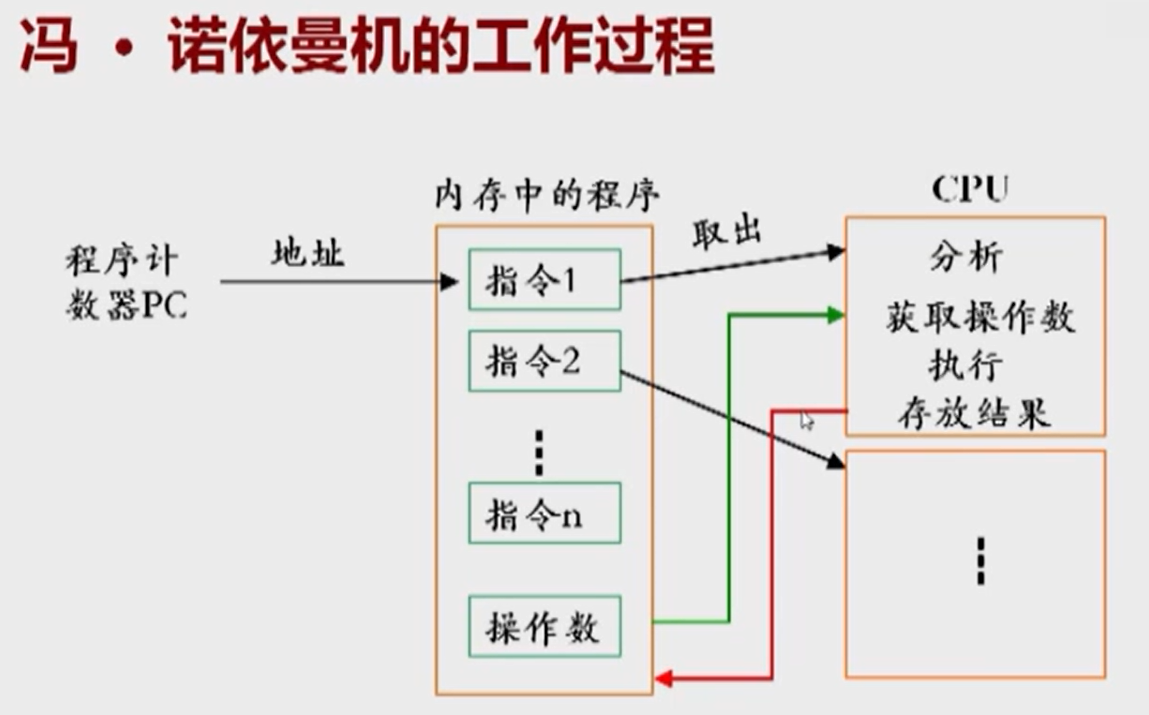
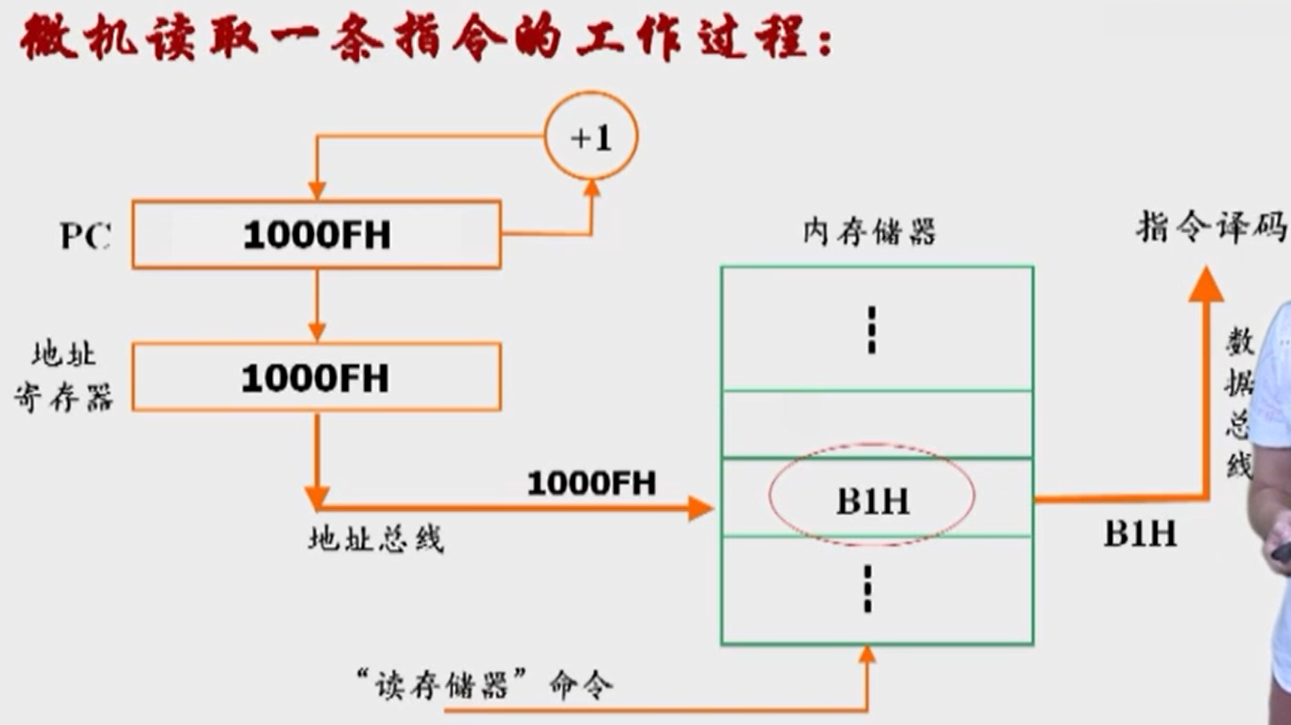
读取一条指令的工作过程
1.将指令所在地址赋给程序计数器PC
2.PC内容送到地址寄存器AR,PC自动加1
3.把AR的内容通过地址总线送至内存储器,经地址译码,选中相应单元
4.CPU的控制器发出读命令
5.在读命令控制下,把所选中单元的内容(即指令操作码)经数据总线送到数据寄存器DR
6.指令译码
- 数据寄存器DR将它送到指令寄存器LR,然后再送到指令译码器LD
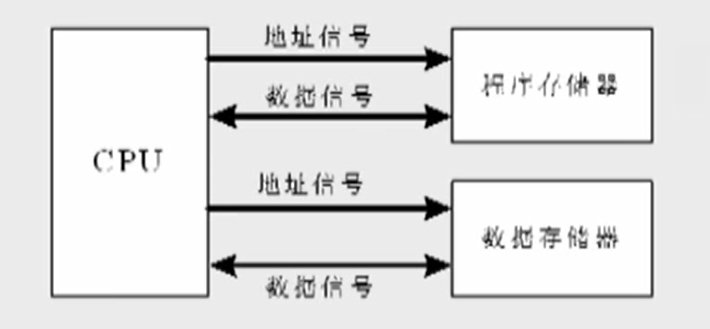
冯诺伊曼计算机体系结构
见图11
冯诺依曼机的特点和不足
特点:
- 程序存储,共享数据,顺序执行
- 属于顺序处理机,适合于确定的算法和数值数据的处理
不足:
- 与存储器间有大量数据交互,对总线要求很高
- 执行顺序由程序决定,对大型复杂任务较困难
- 以运算器为核心,处理效率低
- 由PC控制执行顺序,难以进行真正的并行处理
哈佛结构
指令和数据分别存放在两个独立的存储器模块中
CPU与存储器间指令和数据的传送分别采用两组独立的总线
可以在一个机器周期内同时获得指令操作码和操作数
见图12
计算机中的数制
人类最习惯的计数制是十进制
计算机由具有两种状态的开关器件组成,可以用0和1分别表示两种不同的状态——二进制
- 计算机中采用二进制
- 计算机硬件唯一能够识别的是二进制
任何其他计数制和各种信息要让计算机处理,都需要借助软件转换为二进制
十进制到非十进制数的转换
对二进制的转换:
- 对整数:除2取余
- 对小数:乘2取整
对十六进制的转换:
- 对整数:除16取余
- 对小数:乘16取整
对八进制的转换
- 对整数:除8取余
- 对小数:乘8取整
非十进制数与二进制数的转换
十六进制数与二进制数的转换
- 用4位二进制数表示1位十六进制数
- 整数部分,从小数点向左组,每4位一组,不够4位的高位补0。小数部分,从小数点向右分组,不够4位的在低位补0。
八进制数与二进制数的转换
- 用3位二进制数表示1位八进制数
十六进制(H)、八进制(O)、十进制(D)、二进制(B)
例:
- (二→十) 1011=1×2³+0×2²+1×2¹+1×2⁰
- (十六→十) 5B=5×16¹+11×16⁰
- (十→十六) 25.5=11001.1(B)=19.8(H)
编码
编码
- 信息从一种形式或格式转换为另一种形式的过程
- 用代码来表示各种信息,以便于计算机处理
需要编码的信息种类
- 数值、字符、声音、图形、图像
计算机中的编码
- 数值编码:二进制码、BCD码
- 西文字符编码:ASCII码
BCD码
BCD(Binary Coded DECIMAL)码
- 用二进制表示的十进制数
- 特点:保留十进制的权,数字用0和1表示
8421BCD编码:用4位二进制码表示1位十进制数,每4位之间有一个空格
1010—1111是非法BCD码,只是合法的十六进制数
BCD码与十进制和二进制数之间的转换
- BCD码与十进制数之间存在直接对应关系
- 例:(1001 1000 0110.0011)BCD=986.3
- BCD码与二进制的转换:
- 先转换为十进制数,再转换二进制数;反之同样
BCD码再计算机中的存储方式
以压缩BCD码形式存放:
- 用4位二进制码表示1位BCD码
- 一个存储单元中存放2位BCD数
以扩展BCD码形式存放:
- 用8位二进制码表示1位BCD码,即高4位为0,低四位为有效位
- 每个存储单元存放1位BCD
ASCII码
西文字符编码:将每个字母、数字、标点、控制符用1Byte二进制码表示,其中:标准ASCII的有效位:7bit,最高位默认为0.
ASCII码的奇偶校验
奇校验
- 加上校验位后编码中“1”的个数为奇数。
- 例:A的ASCII码是41H(1000001B)
- 以奇校验传送则为C1H(11000001B)
偶校验
- 加上校验位后编码中“1”的个数为偶数。
- 上例若以偶校验传送,则为41H。
- 加上校验位后编码中“1”的个数为偶数。
计算机中数的表示与运算
数的表示方法:浮点数、定点数
定点数:定点整数、定点小数
- 编程时需要确定小数点位置
- 难以表示两个大小相差较大的数
- 存储空间利用率低
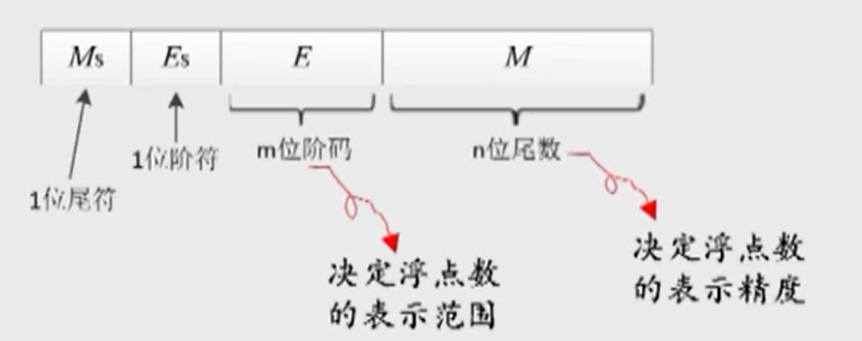
浮点数:小数点的位置可以左右移动的数
规格化浮点数:尾数部分用纯小数表示,即小数点右边第一位不为0
见图13
数的性质(机器数):
无符号数:数中所有的0和1都是数据本身
有符号数:需用0或1表示数的性质(整数或负数)
各种编码视为无符号数,数值多视为有符号数
无符号数的算数运算:
加法运算:1+1=0(有进位)
减法运算:0-1=1(有借位)
乘除法:
- 每乘以2,相对于被乘数向左移动1位
- 每除以2,相对于被除数向右移动1位
00001011×0100=00101100B
00001011:0100=00000010B
有符号数
有符号数:用最高位表示符号,其余是数值
符号数的表示方法:原码、反码、补码(0表示正数、1表示负数)
数的性质右设计者决定:在低级语言程序设计中,根据数的性质右程序语言处理(按无符号数或有符号数处理)
原码
- 最该位为符号位,其余为真值部分。
- 优点:真值和其原码表示之间的对应关系简单,容易理解
- 缺点:
- 计算机中用源码进行加减运算比较困难
- 0的表示不唯一(+0和-0表示为00000000和10000000不唯一)
反码
- 若X>0则,反码=原码
- 若X<0则,反码=原码符号位不变其余取反
补码
若X>0则,补码=反码=原码
若X<0则,补码=反码+1
补码解决了0的唯一性
例:
对模12,有5-4=5+8,-4的补数为12-4=8,所以模12中-4和8互为补数
5-4=5+(-4)=5+(12-4)=5+8=12+1
补码的算数运算:通过引进补码,可将减法运算转换为加法运算。
特殊数10000000
- 无符号数:(10000000)B=128
- 原码:(10000000)B=-0
- 反码:(10000000)B=-127
- 补码:(10000000)B=-128
计算机能力的局限性
计算机的运算能力是有限的
- 计算机无力解决无法设计出算法的问题
- 无法处理无穷运算或连续变化的信息
计算机能够表示的数(表示)的范围是有限的
- 计算机的表数范围受字长的限制,当运算结果超出计算机表数范围时,将产生溢出。
无符号整数的表示范围:
- 当计算机中数的运行结果超出表数范围时,则产生溢出
- 当无符号整数的表数范围:0≤X≦2^n-1^ (n表示字长)
无符号数加减运算溢出的判断方法:当最高位向更高位有进位(或借位)时则产生溢出
有符号整数的表示范围:
原码和反码:-(2^(n-1)^-1)≦X≦(2^n-1^-1)
补码:2^(n-1)^≦X≦2^n-1^-1
对8位二进制数:
- 原码:-127~+127
- 反码:-127~+127
- 补码:-128~+127
符号数运算中的溢出判断
两个有符号二进制数相加或相减时,若运算结果超出可表达范围,则产生溢出
溢出的判断方法:最高位进位状态⊕次高位进位状态-1,则结果溢出
除法运算溢出时,产生“除数为0”中断
乘法运算无溢出问题
基本逻辑运算与逻辑门
逻辑,命题,推理→“或”,“与”,“非”运算
现代计算机由各种逻辑器件构成,数学基础是逻辑代数
“与”运算:同真为真,有假为假。 “.” “∧”
- 与门:对多个逻辑变量执行“与”运算的门电路
“或”运算:有真为真,同假为假。 “+” “∨”
- 或门:对多个逻辑变量执b行“或”运算的门电路
“非”运算:当满足条件时事件不发生,单边运算,只有一个运算对象,运算符为上横线(A=B非)
- 非门:对单个逻辑变量进行运算
算数运算影响高位,逻辑运算、按位运算不影响高位
与门为低电平0时封锁,或门为高电平1时封锁
其他常用逻辑运算及其逻辑电路
与非门:当输入全为1时输出为0,否则输出为1(多输入,单输出)
或非门:当输入全为0时输出为1,否则输出为0(多输入,单输出)
异或逻辑:F=A非×B+A×B非=A⊕B 相同为0,相异为1
- 异或门:当输入值相同时输出为0,不同时输出为1
同或逻辑:F=(A⊕B)非 相同为1,相异为0
- 同或门:当输入值相同时输出为1,不同时输出为0